В.В. Кромер
e-mail: applied@nspu.ru
Арктангенс или логиста?
(К вопросу диахронического скачка)
Под диахроническим скачком понимается динамика употребительности исследуемого лингвистического явления на различных этапах его истории. Целью настоящей работы является построение математической модели диахронического скачка. Модель основывается на нижеследующих положениях.
Лингвистический процесс не
ограничен во времени и развивается во
временном периоде от ![]() до
до ![]() . Причиной процесса является
воздействие на лингвистическую систему,
оказываемое во всем временном периоде
источником лингвистического воздействия (ИЛВ).
Некоторый момент времени t0 является переломным в динамике
процесса. Исследуемое лингвистическое
явление заключается в генерации членами
некоторой группы, далее называемых
генераторами (ГФ), лингвистических форм -
формы 1 (Ф1) либо
формы 2 (Ф2). Функция
ГФ заключается в регулярной генерации
одной из форм - Ф1 или
Ф2. Диахронический
скачок заключается в переходе группы от
преимущественной генерации Ф1 к преимущественной генерации Ф2.
В некоторый момент времени t происходит обращение ГФ,
заключающееся в переходе от генерации
формы Ф1 к
генерации формы Ф2. Расстояние
по временной оси от t до t0 является индивидуальной
характеристикой ГФ. Назовем эту
характеристику лингвистической
инертностью ГФ и обозначим ее за
. Причиной процесса является
воздействие на лингвистическую систему,
оказываемое во всем временном периоде
источником лингвистического воздействия (ИЛВ).
Некоторый момент времени t0 является переломным в динамике
процесса. Исследуемое лингвистическое
явление заключается в генерации членами
некоторой группы, далее называемых
генераторами (ГФ), лингвистических форм -
формы 1 (Ф1) либо
формы 2 (Ф2). Функция
ГФ заключается в регулярной генерации
одной из форм - Ф1 или
Ф2. Диахронический
скачок заключается в переходе группы от
преимущественной генерации Ф1 к преимущественной генерации Ф2.
В некоторый момент времени t происходит обращение ГФ,
заключающееся в переходе от генерации
формы Ф1 к
генерации формы Ф2. Расстояние
по временной оси от t до t0 является индивидуальной
характеристикой ГФ. Назовем эту
характеристику лингвистической
инертностью ГФ и обозначим ее за ![]() .
Инертность может быть
положительной и отрицательной, т.е. часть ГФ
обращается после момента перелома, часть
работает "с опережением", т.е.
обращается ранее момента перелома. На
данном этапе нас интересует математическая
модель явления, и на нарушение принципа
причинности, в соответствии с которым
исключается влияние данного события на все
прошедшие, постараемся не обращать
внимания.
.
Инертность может быть
положительной и отрицательной, т.е. часть ГФ
обращается после момента перелома, часть
работает "с опережением", т.е.
обращается ранее момента перелома. На
данном этапе нас интересует математическая
модель явления, и на нарушение принципа
причинности, в соответствии с которым
исключается влияние данного события на все
прошедшие, постараемся не обращать
внимания.
Как и всякой случайной величине, лингвистической инертности x свойственно некоторое распределение. Рассматриваемое лингвистическое явление относится к разряду социальных явлений. Как показано рядом авторов, все социальные явления - ципфовы, т.е. при больших значениях переменной имеют форму распределения Ципфа [12, с. 113; 10, с. 90]. Запишем выражение для плотности распределения величины x в соответствии с законом Ципфа-Парето [12, с. 115]:
|
|
(1) |
где a - параметр распределения, а A - коэффициент. Принято считать, что ципфовы лишь стационарные (т.е. не содержащие времени) социальные распределения. Распределение (1), несмотря на то, что x имеет размерность времени, также относится к стационарным, поскольку x (инертность ГФ) является некоторой характеристикой исследуемого объекта (ГФ), не зависящей от времени.
Параметр a для социальных явлений
принимает небольшие значения ![]() [10, с. 99-100]. Принимаем наиболее
типичное значение a
= 1, соответствующее закону
Ципфа [12, с. 78].
[10, с. 99-100]. Принимаем наиболее
типичное значение a
= 1, соответствующее закону
Ципфа [12, с. 78].
Выражение (1), распространяемое на
область всех действительных ![]() ,
не вполне корректно, поскольку
не определено при
,
не вполне корректно, поскольку
не определено при ![]() .
Принято считать, что закон
Ципфа-Парето имеет физический смысл лишь
при положительных значениях x, что заставляет вводить
минимальное значение x0
[9, с. 105]. Покажем, что с учетом
характера взаимодействия между группой ГФ
и источником лингвистического воздействия
данная некорректность может быть обойдена.
Плотность распределения p(x) имеет физический смысл
скорости обращения совокупности ГФ. При
.
Принято считать, что закон
Ципфа-Парето имеет физический смысл лишь
при положительных значениях x, что заставляет вводить
минимальное значение x0
[9, с. 105]. Покажем, что с учетом
характера взаимодействия между группой ГФ
и источником лингвистического воздействия
данная некорректность может быть обойдена.
Плотность распределения p(x) имеет физический смысл
скорости обращения совокупности ГФ. При ![]() скорость обращения p(x) согласно (1) бесконечно
возрастает, что нереализуемо физически
ввиду конечности ресурсов любого источника
(источника лингвистического воздействия в
рассматриваемом случае). Формула (1),
рассматриваемая как частное двух величин,
имеет много аналогов в физическом мире, при
этом аналогом величины в знаменателе
являются инертная масса, момент инерции,
электрическое сопротивление,
электрическая проводимость, аналогами
величины в числителе - соответственно
механический импульс, угловой момент,
электрическое напряжение и электрический
ток. Применение моделей, интерпретируемых в
рамках механики Ньютона, с использованием
интуитивно привычных и наглядных понятий (сила,
потенциал, энергия и др.), оказалось
полезным при наукометрическом описании
динамики макропараметров науки и экономики
[1 с. 217]. В данной статье мы воспользуемся
подобным же методом и выявим возможные
аналогии между физическими и социальными
явлениями.
скорость обращения p(x) согласно (1) бесконечно
возрастает, что нереализуемо физически
ввиду конечности ресурсов любого источника
(источника лингвистического воздействия в
рассматриваемом случае). Формула (1),
рассматриваемая как частное двух величин,
имеет много аналогов в физическом мире, при
этом аналогом величины в знаменателе
являются инертная масса, момент инерции,
электрическое сопротивление,
электрическая проводимость, аналогами
величины в числителе - соответственно
механический импульс, угловой момент,
электрическое напряжение и электрический
ток. Применение моделей, интерпретируемых в
рамках механики Ньютона, с использованием
интуитивно привычных и наглядных понятий (сила,
потенциал, энергия и др.), оказалось
полезным при наукометрическом описании
динамики макропараметров науки и экономики
[1 с. 217]. В данной статье мы воспользуемся
подобным же методом и выявим возможные
аналогии между физическими и социальными
явлениями.
В физическом мире невозможно сообщить телу внешний импульс без увеличения массы тела [1], однако при подобных взаимодействиях действуют законы сохранения - закон сохранения импульса в данном случае. Для нас важно то, что внешняя "нагрузка" и внутренний параметр "источника" являются одной и той же физической величиной и аддитивны, т.е. складываются (складываются масса тела и масса передатчика импульса, складываются сопротивление электрической нагрузки и внутреннее сопротивление источника электрического напряжения и т.п.).
Перепишем формулу (1) исходя из
характеристики источника лингвистического
воздействия R, имеющей физический смысл
внутреннего сопротивления источника (или
сопротивления канала передачи при
неограниченных ресурсах источника),
одновременно положив ![]() и заменив x на
и заменив x на ![]() :
:
|
|
(2) |
Подобное распределение (в дискретной форме) было предложено М. Кендаллом для аппроксимации другого социального распределения - распределения Брэдфорда (числа публикаций фиксированного профиля по журналам) [8, с. 74]. Распределение (2) является известным распределением Коши [4, с. 62] с плотностью
|
|
(3) |
и функцией распределения
|
|
(4) |
где ![]() и
и ![]() - параметры.
- параметры.
Выражение (4) для моделирования
диахронического скачка было предложено в
работе [5, с. 369]. Как следует из (2), в
выражениях (3) и (4) значение ![]() является сопротивлением канала
(внутренним сопротивление ИЛВ), а
коэффициент A из выражения (2) является
интенсивностью лингвистического
воздействия и численно равен
является сопротивлением канала
(внутренним сопротивление ИЛВ), а
коэффициент A из выражения (2) является
интенсивностью лингвистического
воздействия и численно равен ![]() исходя из условия нормировки
исходя из условия нормировки 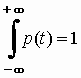 .
Распределение Коши не имеет
моментов положительного порядка, т.е. не
может быть охарактеризовано
математическим ожиданием и стандартным
отклонением, однако ему свойственны мода и
медиана
.
Распределение Коши не имеет
моментов положительного порядка, т.е. не
может быть охарактеризовано
математическим ожиданием и стандартным
отклонением, однако ему свойственны мода и
медиана ![]() и семи-интерквартильная широта
(вероятное отклонение) l. То, что параметр
l является семи-интерквартильной
широтой, непосредственно следует из (4),
поскольку значения F(t) при
и семи-интерквартильная широта
(вероятное отклонение) l. То, что параметр
l является семи-интерквартильной
широтой, непосредственно следует из (4),
поскольку значения F(t) при ![]() и
и ![]() соответственно равны 0,25 и 0,75.
соответственно равны 0,25 и 0,75.
Анализ физических аналогов
формулы (2) позволяет выявить инвариант
любого лингвистического воздействия в
соответствии с (3). Величина ![]() имеет физический смысл
максимальной механической или
электрической мощности источника (импульса,
напряжения и пр.). Аналогично значение
имеет физический смысл
максимальной механической или
электрической мощности источника (импульса,
напряжения и пр.). Аналогично значение 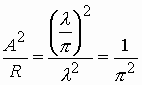 может быть интерпретировано
как мощность источника лингвистического
воздействия. Видно, что мощность источника
инвариантна относительно параметров l
и
t0. Эволюция лексической системы
может рассматриваться как осуществление
ряда диахронических скачков с некоторым
спектром значений l и t0. Возможно графическое
представление эволюции на плоскости в
координатах t0 и l
(рис. 1).
может быть интерпретировано
как мощность источника лингвистического
воздействия. Видно, что мощность источника
инвариантна относительно параметров l
и
t0. Эволюция лексической системы
может рассматриваться как осуществление
ряда диахронических скачков с некоторым
спектром значений l и t0. Возможно графическое
представление эволюции на плоскости в
координатах t0 и l
(рис. 1).

Рис. 1.
Растянутое по времени лингвистическое событие (диахронический скачок) изображается на рис. 1 одной точкой, например точкой 2. Координата t02 точки характеризует момент "перелома" лингвистической ситуации (F(t02) = 0,5). Левее отметки t02 преобладает первая форма, правее - вторая. Координата l2 точки является семи-интерквартильной широтой. Чем больше l, тем растянутее процесс по времени. Линии, проведенные из точки под углом 45° и параллельные первой и второй биссектрисе координатного угла, отсекают на оси t0 точки, в которых значения функции F(t) равны соответственно 0,25 и 0,75.
Мгновенная мощность лингвистического процесса равна
|
|
(5) |
а интегральная энергия лингвистического процесса составляет
|
|
(6) |
Таким образом, параметр l может быть интерпретирован как энергия лингвистического преобразования (с точностью до коэффициента пропорциональности). Из (6) следует, что вялотекущий лингвистический процесс (с большой семи-интерквартильной широтой) требует больших затрат энергии для своей реализации. Следует отметить, что размерности используемых лингвистических величин "мощность" и "энергия" не соответствуют размерностям своих физических аналогов. Размерности лингвистических величин приведены в таблице 1.
Таблица 1
|
Величина |
P |
t0 |
l |
A |
E |
R |
|
Размерность |
|
|
|
|
|
|
Из (4) следует, что
|
|
(7) |
Выразим ![]() через F(t):
через F(t):
|
|
(8) |
Итак, аналитическое выражение
для диахронического скачка (4) является
решением дифференциального уравнения
![]() .
.
Разложение cos x в степенной ряд дает
|
|
(9) |
откуда при учете первых 2 членов разложения получаем:
|
|
(10) |
Выражение (10) выполняется точно в
окрестности ![]() . Для нахождения
. Для нахождения
![]() в окрестности
в окрестности
![]() преобразуем (8):
преобразуем (8):
|
|
(11) |
Разложение sin x в степенной ряд дает
|
|
(12) |
откуда при учете первого члена разложения получаем
|
|
(13) |
Из соображений симметрии следует,
что в окрестности ![]()
|
|
(14) |
Совместное рассмотрение (10), (13) и (14) позволяет высказать предположение, что решение дифференциального уравнения
|
|
(15) |
где r - некоторый коэффициент, в первом приближении соответствует функции диахронического скачка (4).
В работе [13] указывается, что функцию (4) трудно обосновать теоретически, "since the arc tan function does not appear as the solution of a simple differential equation"; (цитируется по [16, с. 100]). И далее в работе [13] для описания диахронического скачка предложено дифференциальное уравнение
|
|
(16) |
где r - коэффициент пропорциональности.
Разница между дифференциальными уравнениями (15) и (16) заключается лишь в том, что согласно (16) приращение новых форм пропорционально доле используемых новых форм и доле еще используемых старых форм, а согласно (15), это приращение пропорционально квадрату доли новых форм и квадрату доли старых форм. Решением дифференциального уравнения (16) является логистическая функция распределения
|
|
(17) |
а аналитическое выражение для диахронического скачка (17) в работе [13] предложено назвать законом Пиотровского. Подобная модель известна в эпидемиологии и описывает рост биологической популяции в условиях ограниченного жизненного пространства. В работе [14] утверждается, что логистическое распределение не играет никакой выдающейся роли в описании процессов развития, а самые противоречивые теоретические модели могут быть подтверждены на одном и том же материале; (цитируется по [7, с. 68-69]).
На наш взгляд, 2-я степень при F(t) в дифференциальном уравнении (15) отражает социальный характер рассматриваемых отношений (порядок связей на 1 выше порядка связей при биологическом характере отношений). Решением дифференциального уравнения (15) является выражение
|
|
(18) |
где F(t) задано неявно. Члены
 и
и ![]() и определяют ципфовский (обратно
пропорциональный) характер зависимости F(t)
при больших значениях
и определяют ципфовский (обратно
пропорциональный) характер зависимости F(t)
при больших значениях ![]() .
.
На рис. 2 представлены графики зависимостей по выражениям (4) - тонкой линией, (17) - жирной линией и (18) - штриховой линией.
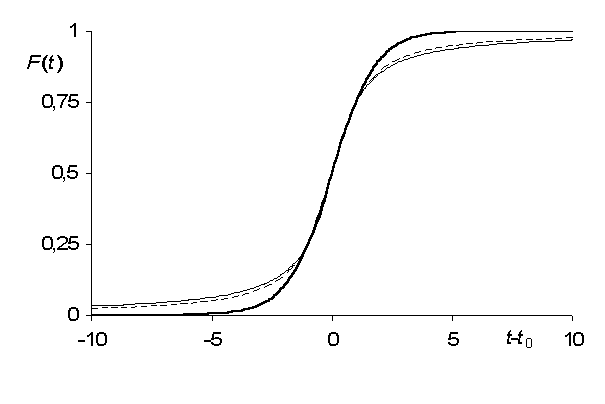
Рис. 2.
Все 3 зависимости нормированы
таким образом, чтобы совпадали вероятные
отклонения, т.е. по определению совпадают
все 4 квартиля. Видно, что зависимости (4) и (18)
близки, в то время как зависимость (17) (логиста)
слишком быстро устремляется к 0 и
соответственно к 1 при возрастании модуля ![]() .
.
Ранее было показано, что мощность
источника лингвистического воздействия
инвариантна относительно l, т.е. внутреннее сопротивление
источника R функционально зависит от
интенсивности источника A, что обеспечивает постоянство
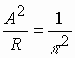 . Может быть предложено
следующее объяснение этого явления: любое
лингвистическое воздействие
осуществляется неким модулем,
скомпонованным из определенного,
неизменного количества субмодулей.
Субмодули соединяются в общем случае
последовательно-параллельно, при этом при
последовательном соединении субмодулей
суммируются их интенсивности и внутренние
сопротивления, при параллельном же
соединении суммируются проводимости (величины,
обратные внутренним сопротивлениям) при
неизменности интенсивности. Аддитивность
параметров субмодулей (интенсивности и
внутреннего сопротивления) обеспечивает
необходимое постоянство максимальной
мощности источника лингвистического
воздействия. [2]
. Может быть предложено
следующее объяснение этого явления: любое
лингвистическое воздействие
осуществляется неким модулем,
скомпонованным из определенного,
неизменного количества субмодулей.
Субмодули соединяются в общем случае
последовательно-параллельно, при этом при
последовательном соединении субмодулей
суммируются их интенсивности и внутренние
сопротивления, при параллельном же
соединении суммируются проводимости (величины,
обратные внутренним сопротивлениям) при
неизменности интенсивности. Аддитивность
параметров субмодулей (интенсивности и
внутреннего сопротивления) обеспечивает
необходимое постоянство максимальной
мощности источника лингвистического
воздействия. [2]
Выше рассматривался вариант диахронического скачка с полным вытеснением старых форм новыми. В случае неполного вытеснения старых форм новыми Г. Альтманном предложено описывать процесс уравнением
|
|
(19) |
где ![]() - параметр, характеризующий
процесс [13]; (цитируется по [16, с. 101]).
Выражение (19) эквивалентно
- параметр, характеризующий
процесс [13]; (цитируется по [16, с. 101]).
Выражение (19) эквивалентно
|
|
( |
В данном выражении и последующих F(t)
не является функцией
распределения, поскольку ![]() .
За F(t) обозначена доля новых форм в
данном синхронном срезе. Соответственно
будем говорить не о плотности вероятности p(t),
а о скорости обращения ГФ. В
рамках модели диахронического скачка,
предложенной в данной статье,
диахронический скачок с неполным
вытеснением старых форм новыми может быть
объяснен нехваткой материала для
компоновки модуля лингвистического
воздействия. Выпишем выражения,
характеризующие процесс в данном случае.
.
За F(t) обозначена доля новых форм в
данном синхронном срезе. Соответственно
будем говорить не о плотности вероятности p(t),
а о скорости обращения ГФ. В
рамках модели диахронического скачка,
предложенной в данной статье,
диахронический скачок с неполным
вытеснением старых форм новыми может быть
объяснен нехваткой материала для
компоновки модуля лингвистического
воздействия. Выпишем выражения,
характеризующие процесс в данном случае.
Введем q
- коэффициент нехватки
материала для компоновки модуля ИЛВ.
Мощность ИЛВ определится в данном случае
как  , откуда
, откуда 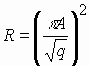 .
Скорость обращения ГФ составит
.
Скорость обращения ГФ составит
|
|
(20) |
а доля новых форм равна, с учетом
начального условия ![]()
|
|
(21) |
За l обозначено ![]() .
Здесь l
- половина расстояния по
временной оси между уровнями F(t) в 0,25 и 0,75 от максимального
значения F(t), равного
.
Здесь l
- половина расстояния по
временной оси между уровнями F(t) в 0,25 и 0,75 от максимального
значения F(t), равного ![]() согласно (21). Видно, что в случае
нехватки материала для компоновки модуля
ИЛВ диахронический скачок в динамике
следует функции арктангенса, при этом
согласно (21). Видно, что в случае
нехватки материала для компоновки модуля
ИЛВ диахронический скачок в динамике
следует функции арктангенса, при этом ![]() рационально обозначить за c для единства обозначений с (19) и
(
рационально обозначить за c для единства обозначений с (19) и
(![]() ).
).
Мощность процесса в соответствии с (5) составит
|
|
(22) |
Интегральная энергия процесса равна
|
|
(23) |
Итак, при необходимости реализации процесса с неполным завершением перехода от формы Ф1 к форме Ф2 энергия процесса составляет долю q от энергии полномасштабного процесса при инвариантности семи-интерквартильного размаха.
Модель допускает обобщение на случай q > 1, т.е. при избытке субмодулей в компонуемом модуле. Из выражения (21) можно найти время tf полного завершения процесса, приравняв F(t) = 1.
|
|
(24) |
На рис. 3 приведены примеры
диахронических скачков для разных значений
![]() (с =
0,5 - штриховая линия; c
= 1 - жирная линия; c
= 2 - тонкая линия).
(с =
0,5 - штриховая линия; c
= 1 - жирная линия; c
= 2 - тонкая линия).
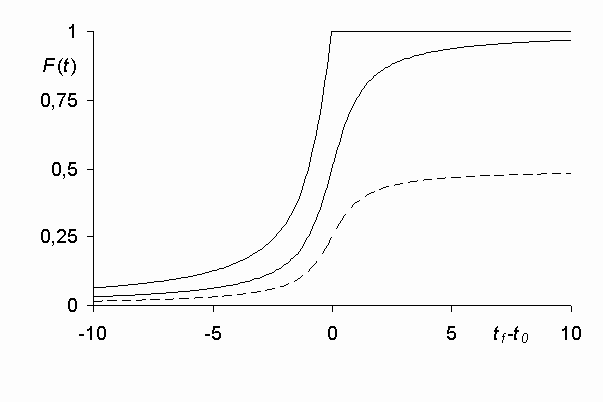
Рис. 3.
Зависимости, связанные с законами Ципфа-Мандельброта и Менцерата-Альтманна, красноречиво свидетельствуют в пользу существования синергетических механизмов саморегуляции [6, с. 134]. Статистика диахронического скачка также представляет интерес для выработки исчисляемых параметров динамических синергетических моделей [6, с. 174]. В наших работах [2, 3] была сделана попытка параметризации русского и английского языков (на основе данных частотных словарей соответственно [11] и [15]) с использованием ядерно-веерной модели вертикального распределения слов [2]. Было предложено аппроксимировать вероятность слова с рангом i в частотном списке функцией [2, с. 6]
|
|
(25) |
где M - нормирующий множитель, s - поправка Ворончака, а Bi - корректив частых слов, функционально зависящий от i согласно выражения [2, с. 5].
|
|
(26) |
где B1, B2 и a - параметры зависимости, i0 - ранг точки перегиба функции Bi. В рассматриваемой работе влияние Bi на pi рассматривается как вставка в формулу (25) данной работы неких фиктивных рангов, природа коих проистекает из процесса слияния отдельных подвыборок в общую выборку. В настоящей работе делается предположение, что синергетические механизмы вставки фиктивных рангов и реализации диахронического скачка идентичны, т.е. тот и другой являются ципфовыми с наложенными ограничениями на мощность источника, ответственного за процесс. Анализ численных значений параметра a и его дисперсии из зависимости (26) согласно [2, 3] позволяет высказать предположение, что a = 1, а флуктуации измеренных значений a имеют статистическую природу. Перепишем (26) исходя из a = 1 в форме
|
|
(27) |
где Bm
- максимальное значение Bi
(при ![]() . Мощность источника воздействия
по прежнему равна
. Мощность источника воздействия
по прежнему равна ![]() (в единицах Bm), однако для сравнения
типологически отличающихся языков удобно
измерять мощность значением
(в единицах Bm), однако для сравнения
типологически отличающихся языков удобно
измерять мощность значением ![]() .
Это значение составляет 43 для
русского и 160 для английского языков.
.
Это значение составляет 43 для
русского и 160 для английского языков.
Интегральная энергия процесса
составляет ![]() единиц
Bm. Размерность мощности
рассматриваемого процесса по-прежнему
безразмерна, энергия же процесса равна
единиц
Bm. Размерность мощности
рассматриваемого процесса по-прежнему
безразмерна, энергия же процесса равна ![]() и измеряется в логарифмических
единицах (нитах)[3], т.е.
имеет размерность энтропии. Поскольку в
формуле (27) аргументом арктангенса является
и измеряется в логарифмических
единицах (нитах)[3], т.е.
имеет размерность энтропии. Поскольку в
формуле (27) аргументом арктангенса является
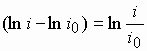 , логарифм ранга является
естественной единицей измерения при
оперировании с рангами. Для ципфовской
выборки энергия процесса равна 0, поскольку Bm
= 0. Для неципфовской выборки
энергия процесса отражает тематическое
богатство выборки.
, логарифм ранга является
естественной единицей измерения при
оперировании с рангами. Для ципфовской
выборки энергия процесса равна 0, поскольку Bm
= 0. Для неципфовской выборки
энергия процесса отражает тематическое
богатство выборки.
Литература
1. Брусиловский Б.Я. Математические модели в прогнозировании и организации науки. Киев: Наукова думка, 1975.
2. Кромер В.В. Ядерно-веерная модель вертикального распределения слов в русском языке / Новосибирский гос. пед. ун-т. Новосибирск, 1997. Деп. в ИНИОН РАН 31.03.97, № 52458.
3. Кромер В.В. Подпорно-экспоненциальная модель генеральной лексической совокупности английского языка / Новосибирский гос. пед. ун-т. Новосибирск, 1997. Деп. в ИНИОН РАН 18.12.97, № 53134.
4. Математическая энциклопедия / Гл. ред. И.М. Виноградов. М.: Сов. Энциклопедия, 1982. Т. 3.
5. Пиотровская А.А., Пиотровский Р.Г. Математические модели диахронии и текстообразования // Статистика речи и автоматический анализ текста. Л.: Наука, 1974. С. 361-400.
6. Пиотровский Р.Г. Лингвистический автомат (в исследовании и непрерывном обучении). СПб.: Изд-во РГПУ, 1999.
7. Феллер В. Введение в теорию вероятностей и ее приложения. В 2-х томах. Пер. с англ. М.: Мир, 1984. Т. 2.
8. Хайтун С.Д. Наукометрия: Состояние и перспективы. М.: Наука, 1983.
9. Хайтун С.Д. Проблемы количественного анализа науки. М.: Наука, 1989.
10. Хайтун С.Д. Мои идеи. М.: Агар, 1998.
11. Частотный словарь русского языка / Под ред. Л.Н. Засориной М.: Русский язык, 1977.
12. Яблонский А.И. Модели и методы исследования науки. М.: Эдиториал УРРС, 2001.
13. Altmann G., Buttlar H., Rott W., Strauss U. A law of language change // Historical Linguistics (Quantitative Linguistics, Vol. 18). Bochum: Brockmeyer, 1983.
14. Feller W. On the logistic law of growth and its empirical verifications in biology // Acta Biotheoretica. 1940. Vol. 5. P. 51-66.
15. Kučera H., Francis W.H. Computational Analysis of Present-Day American English. Providence, 1967.
16. Leopold E. Stochastische Modellierung lexikalischer Evolutionsprozesse. Hamburg: Verlag Dr. Kovač, 1998.
Сноски
1. Самый простой пример: при попадании снаряда-болванки в вагон с песком (случай неупругого соударения) вагону будет передан импульс снаряда и он придет в движение, однако масса вагона увеличится на массу снаряда. (обратно в текст)
2. Полным аналогом схемы компоновки источника лингвистического воздействия является компоновка электрических батарей из элементов питания путем их последовательно-параллельного соединения. (обратно в текст)
3. 1 нит = log2e = 1,443 бита. (обратно в текст)

 ,
,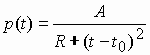 .
.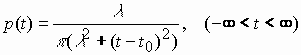
 ,
, .
.
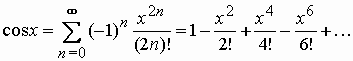 ,
,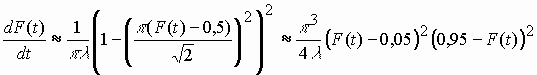 .
. .
. ,
,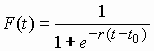 ,
,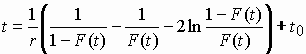 ,
, ,
, ,
,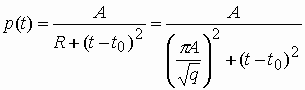 ,
,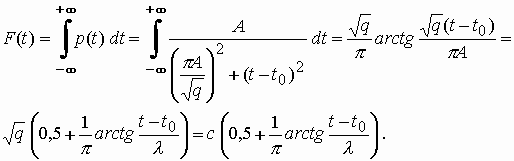
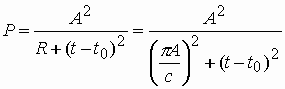 .
.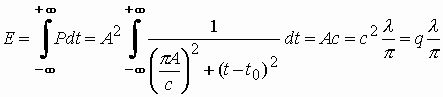 .
. .
.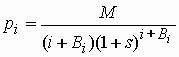 ,
,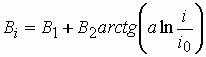 ,
,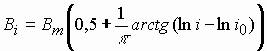 ,
,